Space colonization

First developed in [RFLF05], the space colonization algorithm was thought to model leaf venation before being successfully applied to generate trees [RLP07].

The general idea of the algorithm is not, contrary to Weber and Penn or L-system, to model trees from a set of describing parameters but to deduce the branching structure from a set of attraction points.

Steps

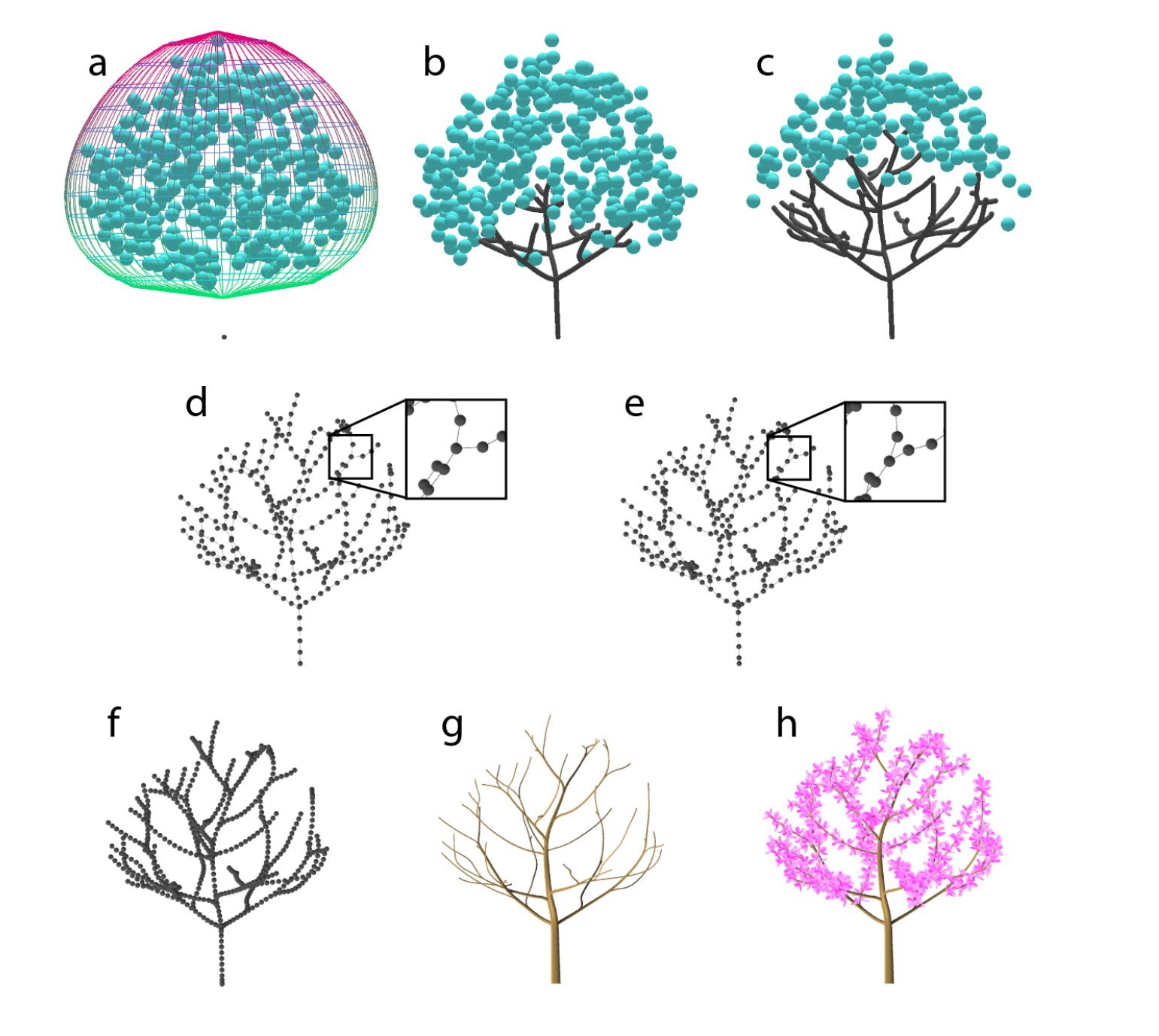
The first step of the algorithm is generate the set of attractration and to position the first node (figure 1 a)). Then the tree will grow until the node reaches the attraction point (b, c). This method has a tendency to generate more branch a tree normally possess and these branches are likely to contain unnatural twists. Hence, the nodes are decimate and are adjust to correct the the branching angles (d, e). Then the radius of each stem is deduce from tree height to set the starting radius, then children node radius is computed according to the pipe model developed in [SYHK64]. The idea behind the pipe model is that at each branching the surface of the branches remains constant.

where ] is a parameter of the method, is radius of the supporting node and and are the node supported by .

In this form this equation has an infinity of solution as and are unknown. In my implementation of the algorithm the radius of is proportional to the angle between the direction of and the direction of this allows to have a trunk bigger than the branches it supports.

Then the mesh is created by constructing generalized cylinder around the nodes and organs (leaves, blossom) are added to the tree (g, h).

Figure 1. steps of the space colonization methods

Algorithm

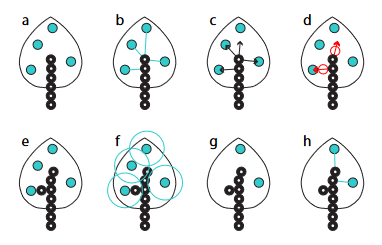
The algorithm used to generated tree node is the following. At every iteration, for each node the attraction points close of a distance inferior or to influence_radius are considered to be influence points. If the set of influence points is not empty compute a new node where is the step_size parameter and

Then if reaches an attraction point this point is removed from the list.

Figure 2. algorithm

Performence

The algorithm need to calculated distances between two point clouds at each iteration. A naive approach has complexity at each iteration, where is the number of tree nodes and is the number of attraction points. Using an octree, this complexity can be reduces to .

This algorithm takes more time than the two previous methods but as the advantage to match the envelope it was given. This approach is more fit to our needs as we want to deduce the shape of the tree for the elevation of the canopy.